We present our work on designing an aggregatable distributed key generation algorithm, which will appear at Eurocrypt 2021. This is joint work with Kobi Gurkan, Philipp Jovanovic, Mary Maller, Sarah Meiklejohn, Gilad Stern, and Alin Tomescu.
What is a Distributed Key Generation Algorithm?
Ever heard of Shamir’s secret sharing algorithm? It’s a classic. The overriding idea is that it is harder to corrupt many people than corrupting one person. Shamir’s secret sharing algorithm ensures that you can only learn a secret if multiple people cooperate. In cryptography, we often want to share a secret key so that we can distribute trust. The secret key might be used to decrypt a database, sign a transaction, or compute some pseudo-randomness.
In a secret sharing scheme, there is a trusted dealer who knows the whole secret, shares it out, and then goes offline. This begs the question: why bother to share the secret in the first place if you have a trusted dealer who knows the whole secret? Often the reason is that the secret sharing scheme is merely being used as an ingredient in a larger distributed key generation algorithm in which nobody knows the full secret. This isn’t always true; certainly, there are cases where a central authority might delegate tasks to workers with less authority. But in the case where there is no central authority, we need a more complete solution.
A distributed key generation algorithm allows a set of n users to jointly generate a public key. Any subset of size t+1 can reconstruct the secret key (where t is some predetermined threshold). No subset of size t or less can reconstruct. Typically DKGs consist of n parallel instances of a secret sharing scheme. We run n parallel instances of the Scrape secret sharing scheme.
What is special about this DKG?
Many things are special about our DKG, but probably the biggest advantage is that we do not require “complaints rounds”. The state-of-the-art for DKGs assumes that there is a private communication channel between all participants. The shares of the secret key are sent over these private communication channels and are verified only by the intended recipients. This means that if an honest party does not receive their secret share, they are expected to publicly broadcast a complaint (during the complaints round) against the faulty party.
The absence of a complaints round reduces overheads resulting in a faster DKG. In a Pedersen DKG, participants must be allowed enough time to submit their complaints in order to disqualify malicious participants. These participants might be subject to network failures and denial-of-service attacks, so this round can’t be too short. We do not make efficiency sacrifices in order to remove the complaints round, indeed asymptotically, our DKG is faster than the Pedersen DKG. There are two reasons for the efficiency:
- Our DKG is publicly verifiable.
- Our DKG is aggregatable.
By publicly verifiable, we mean that anyone, at any time, can check that the outcome of the DKG is valid. This includes people that may have had nothing to do with the key generation algorithm. There is no need for parties to reach a consensus to decide who has and has not misbehaved.
As a consequence of public verifiability, we have that participants who were offline during the entire run of the protocol can still obtain their share without hurting the secrecy of the joint secret key, even if these participants haven’t submitted their contributions. For example, if we have a threshold t, we only require t+1 participants to submit their contributions for the secrecy property to hold.
What does aggregatable mean, and why is it important?
Aggregatability basically means all the information required by a participant to obtain their secret share, or for a verifier to check the output, is linear in the number of players. This is a great improvement over prior works – which were quadratic.
When a party contributes to the public key, they produce a share of size m. This share allows other parties to learn their part of the secret. It also demonstrates that the party has behaved honestly. So if two parties output two contributions, that means we must read two shares, costing us 2m work then? Surely? Well, no. In our scheme, we can aggregate the two parties contributions into a single share of size m and still retain all the required information to obtain secrets and verify results. Likewise, we can aggregate 4, 8, 1001 shares, etc., and still only have a transcript of size m (like BLS signatures, if you are familiar with those).
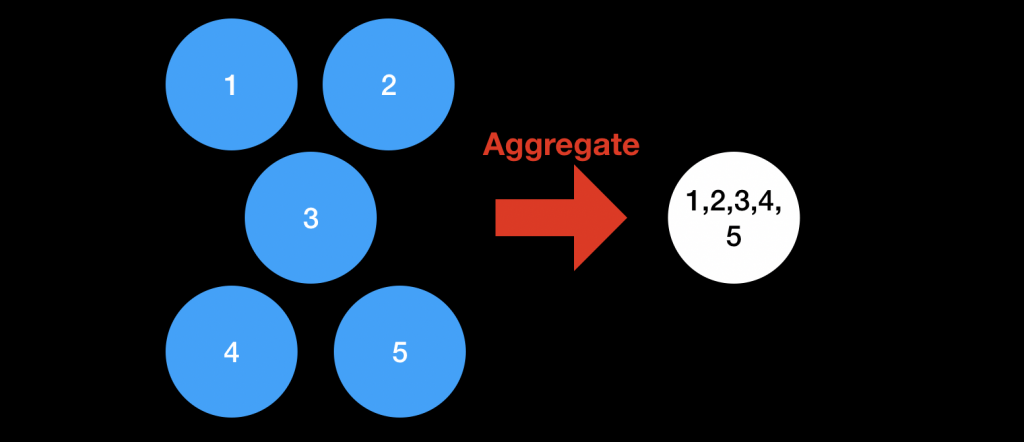
Okay, so we can aggregate, and this saves space and verifier work. “Or does it?” you might be thinking. Somebody has to aggregate these shares. If you send them all to one party, doesn’t that one party need to do one very large aggregation?
Again, the answer is no. We do not need to aggregate the shares all in one go. Instead, we can gradually aggregate them. That way, we can split the aggregation work across many different parties.
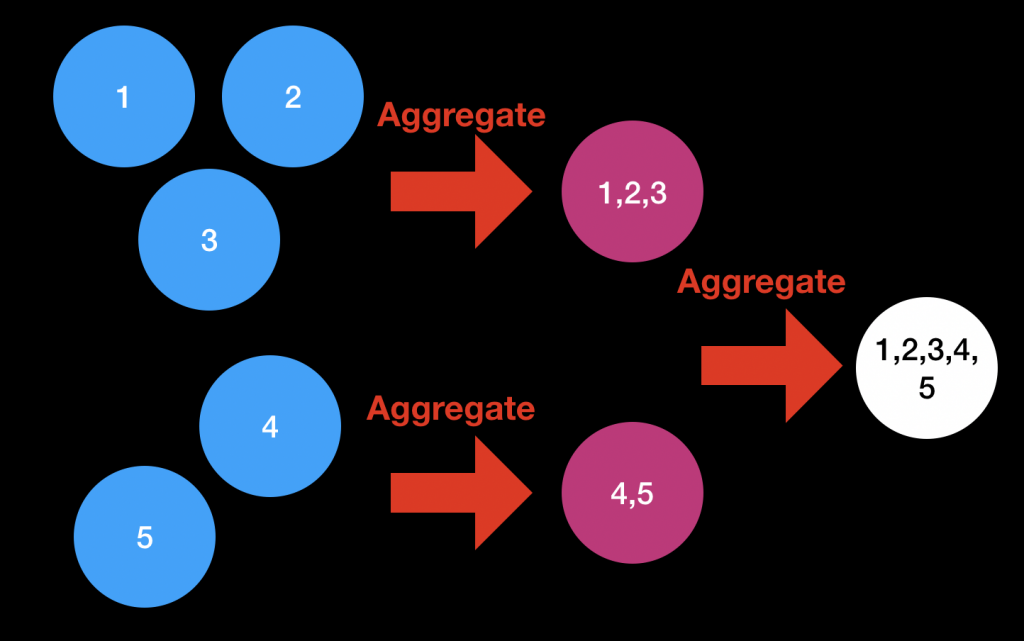
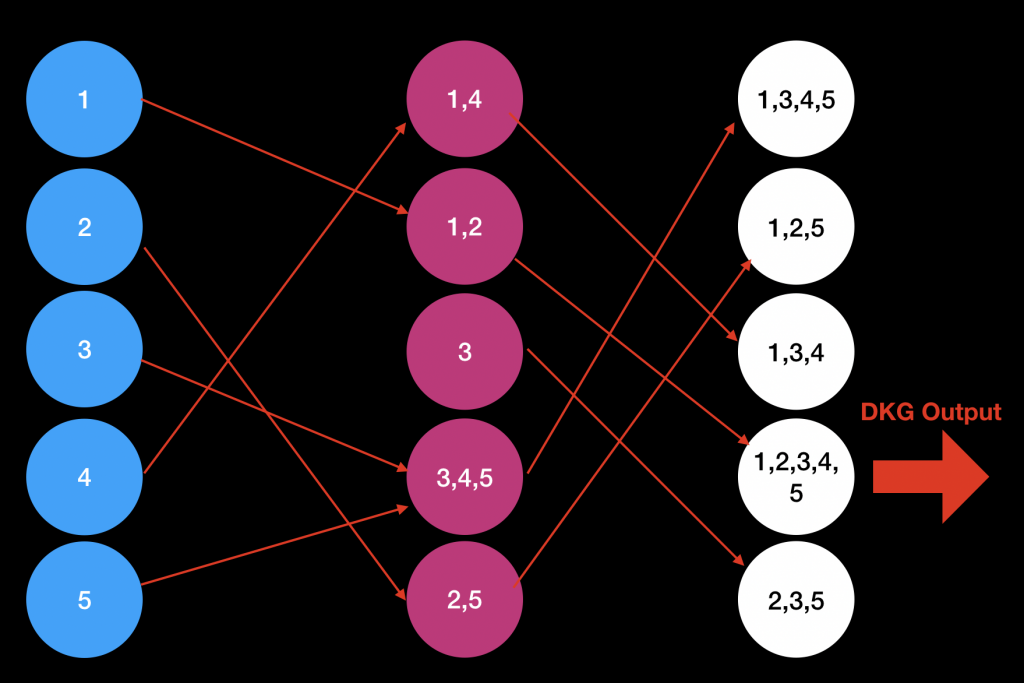
At this point, you might be wondering how to order the aggregations to minimise the total amount of work. Perhaps the aggregators could be arranged in a tree-like structure. This solution is great if you can trust the aggregators not to go offline, but what if you can’t?
We instead decided to carry out the aggregation via a “gossip” protocol. Parties randomly select who to send their shares to. If they receive a share, then they update their share to the aggregation of their current share and the new share (provided everything verifies). Once one party has enough contributions in their share, they broadcast it as the final DKG transcript to all the other players.
Our DKG is very well suited to this gossiping method of aggregation. In particular, it is okay to aggregate the same contribution over and over again.
Is this relevant for random beacons?
Yes, our results are highly relevant to random beacons. Currently, Drand is implementing a random beacon built from the Pedersen DKG and BLS signatures – an idea initially put forward by Dfinity. We cannot directly replace their DKG with our one, but we can if we replace the BLS signatures with an alternative signature scheme.
To explain, the secret key for a BLS signature is a field element. Our DKG outputs secrets which are group elements, and thus it cannot be used for BLS signatures. However, these techniques are not limited to using BLS. They actually work for any “verifiable unpredictable function” or “unique signature scheme”. So, what about using a verifiable unpredictable function that has a group element as a secret key?
We looked far and wide for one of these but did not find anything in the literature. So we decided to make our own. We prove security in the random oracle model under the SXDH assumption and the BDH assumption in Type 3 bilinear groups.
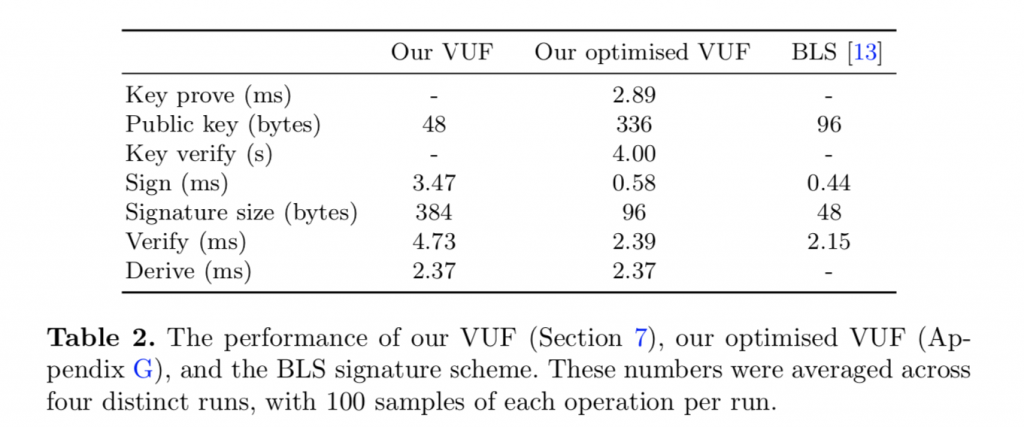
Our signature scheme is not quite as efficient as BLS, but it’s not far off. Signatures are twice the size, and signing and verification time is only fractionally higher. Our public key is 3.5 times larger and must be verified. We also additionally require a “derive” function to obtain the unique components from the signature.
What about applications that your DKG doesn’t work for?
There are many applications that our DKG does not work for. Firstly we output group elements, not field elements. Secondly, we actually require quite a special property for our applications which we call “rekeyability”. However, our proving techniques are highly applicable to other efficient DKGs such as the Pedersen DKG and the Fouque-Stern DKG. We prove that El-Gamal encryption and BLS signatures can be securely implemented under either of these DKGs. Our results do not extend to Schnorr signatures.
The negative result of Gennaro et al. does not apply to us. They show that the Pedersen DKG is not random. We argue that it is random enough to implement certain rekeyable crypto schemes securely. This is not so different from Gennaro et al.’s result that the Pedersen DKG suffices for Schnorr signatures. However, that result has since been attacked, assuming a concurrent adversary. Our proof techniques are entirely different and do not rely on rewinding the adversary.
As a result, the simpler Pedersen DKG for threshold BLS signatures can now be used safely without implementing complex multi-phase protocols, which can be harder to code correctly and error-prone. Full details can be found in our paper.